И зачем она нужна. Мы уже знаем, что такое система отсчета, относительность движения и материальная точка. Что ж, пора двигаться дальше! Здесь мы рассмотрим основные понятия кинематики, соберем вместе самые полезные формулы по основам кинематики и приведем практический пример решения задачи.
Решим такую задачу: точка движется по окружности радиусом 4 метра. Закон ее движения выражается уравнением S=A+Bt^2. А=8м, В=-2м/с^2. В какой момент времени нормальное ускорение точки равно 9 м/с^2? Найти скорость, тангенциальное и полное ускорение точки для этого момента времени.
Решение: мы знаем, что для того, чтобы найти скорость нужно взять первую производную по времени от закона движения, а нормальное ускорение равняется частному квадрата скорости и радиуса окружности, по которой точка движется. Вооружившись этими знаниями, найдем искомые величины.
Нужна помощь в решении задач? Профессиональный студенческий сервис готов оказать ее.
Это векторная физическая величина, численно равная пределу, к которому стремится средняя скорость за бесконечно малый промежуток времени:
Другими словами, мгновенная скорость – это радиус-вектора по времени.
Вектор мгновенной скорости всегда направлен по касательной к траектории тела в сторону движения тела.
Мгновенная скорость дает точную информацию о движении в определенный момент времени. Например, при езде в автомобиле в некоторый момент времени водитель смотрит на спидометр и видит, что прибор показывает 100 км/ч. Через некоторое время стрелка спидометра указывает на величину 90 км/ч, а еще спустя несколько минут – на величину 110 км/ч. Все перечисленные показания спидометра – это значения мгновенной скорости автомобиля в определенные моменты времени. Скорость в каждый момент времени и в каждой точке траектории необходимо знать при стыковке космических станций, при посадке самолетов и т.д.
Имеет ли понятие «мгновенной скорости» физический смысл? Скорость – это характеристика изменения в пространстве. Однако, для того, чтобы определить, как изменилось перемещение, необходимо наблюдать за движением в течение некоторого времени. Даже самые совершенные приборы для измерения скорости такие как радарные установки, измеряют скорость за промежуток времени – пусть достаточно малый , однако это все-таки конечный временной интервал, а не момент времени. Выражение «скорость тела в данный момент времени» с точки зрения физики не является корректным. Однако, понятие мгновенной скорости очень удобно в математических расчетах, и им постоянно пользуются.
Примеры решения задач по теме «Мгновенная скорость»
ПРИМЕР 1
ПРИМЕР 2
| Задание | Закон движения точки по прямой задается уравнением . Найти мгновенную скорость точки через 10 секунд после начала движения. |
| Решение | Мгновенная скорость точки – это радиус-вектора по времени. Поэтому для мгновенной скорости можно записать:
Через 10 секунд после начала движения мгновенная скорость будет иметь значение: |
| Ответ | Через 10 секунд после начала движения мгновенная скорость точки м/с. |
ПРИМЕР 3
| Задание | Тело движется по прямой так, что его координата (в метрах) изменяется по закону . Через сколько секунд после начала движения тело остановится? |
| Решение | Найдем мгновенную скорость тела: |
1.2. Прямолинейное движение
1.2.4. Средняя скорость
Материальная точка (тело) сохраняет свою скорость неизменной только при равномерном прямолинейном движении. Если движение является неравномерным (в том числе и равнопеременным), то скорость тела изменяется. Такое движение характеризуют средней скоростью. Различают среднюю скорость перемещения и среднюю путевую скорость.
Средняя скорость перемещения является векторной физической величиной, которую определяют по формуле
v → r = Δ r → Δ t ,
где Δ r → - вектор перемещения; ∆t - интервал времени, за которое это перемещение произошло.
Средняя путевая скорость является скалярной физической величиной и вычисляется по формуле
v s = S общ t общ,
где S общ = S 1 + S 1 + ... + S n ; t общ = t 1 + t 2 + ... + t N .
Здесь S 1 = v 1 t 1 - первый участок пути; v 1 - скорость прохождения первого участка пути (рис. 1.18); t 1 - время движения на первом участке пути и т.п.
Рис. 1.18
Пример 7. Одну четверть пути автобус движется со скоростью 36 км/ч, вторую четверть пути - 54 км/ч, оставшийся путь - со скоростью 72 км/ч. Рассчитать среднюю путевую скорость автобуса.
Решение. Общий путь, пройденный автобусом, обозначим S :
S общ = S .
S 1 = S /4 - путь, пройденный автобусом на первом участке,
S 2 = S /4 - путь, пройденный автобусом на втором участке,
S 3 = S /2 - путь, пройденный автобусом на третьем участке.
Время движения автобуса определяется формулами:
- на первом участке (S
1 = S
/4) -
t 1 = S 1 v 1 = S 4 v 1 ;
- на втором участке (S
2 = S
/4) -
t 2 = S 2 v 2 = S 4 v 2 ;
- на третьем участке (S
3 = S
/2) -
t 3 = S 3 v 3 = S 2 v 3 .
Общее время движения автобуса составляет:
t общ = t 1 + t 2 + t 3 = S 4 v 1 + S 4 v 2 + S 2 v 3 = S (1 4 v 1 + 1 4 v 2 + 1 2 v 3) .
v s = S общ t общ = S S (1 4 v 1 + 1 4 v 2 + 1 2 v 3) =
1 (1 4 v 1 + 1 4 v 2 + 1 2 v 3) = 4 v 1 v 2 v 3 v 2 v 3 + v 1 v 3 + 2 v 1 v 2 .
v s = 4 ⋅ 36 ⋅ 54 ⋅ 72 54 ⋅ 72 + 36 ⋅ 72 + 2 ⋅ 36 ⋅ 54 = 54 км/ч.
Пример 8. Пятую часть времени городской автобус тратит на остановки, остальное время он движется со скоростью 36 км/ч. Определить среднюю путевую скорость автобуса.
Решение. Общее время движения автобуса на маршруте обозначим t :
t общ = t .
t 1 = t /5 - время, затраченное на остановки,
t 2 = 4t /5 - время движения автобуса.
Путь, пройденный автобусом:
- за время t
1 = t
/5 -
S 1 = v 1 t 1 = 0,
так как скорость автобуса v 1 на данном временном интервале равна нулю (v 1 = 0);
- за время t
2 = 4t
/5 -
S 2 = v 2 t 2 = v 2 4 t 5 = 4 5 v 2 t ,
где v 2 - скорость автобуса на данном временном интервале (v 2 = = 36 км/ч).
Общий путь автобуса составляет:
S общ = S 1 + S 2 = 0 + 4 5 v 2 t = 4 5 v 2 t .
Вычисление средней путевой скорости автобуса произведем по формуле
v s = S общ t общ = 4 5 v 2 t t = 4 5 v 2 .
Расчет дает значение средней путевой скорости:
v s = 4 5 ⋅ 36 = 30 км/ч.
Пример 9. Уравнение движения материальной точки имеет вид x (t ) = (9,0 − 6,0t + 2,0t 2) м, где координата задана в метрах, время - в секундах. Определить среднюю путевую скорость и величину средней скорости перемещения материальной точки за первые три секунды движения.
Решение. Для определения средней скорости перемещения необходимо рассчитать перемещение материальной точки. Модуль перемещения материальной точки в интервале времени от t 1 = 0 с до t 2 = 3,0 с вычислим как разность координат:
| Δ r → | = | x (t 2) − x (t 1) | ,
Подстановка значений в формулу для вычисления модуля перемещения дает:
| Δ r → | = | x (t 2) − x (t 1) | = 9,0 − 9,0 = 0 м.
Таким образом, перемещение материальной точки равно нулю. Следовательно, модуль средней скорости перемещения также равен нулю:
| v → r | = | Δ r → | t 2 − t 1 = 0 3,0 − 0 = 0 м/с.
Для определения средней путевой скорости нужно рассчитать путь, пройденный материальной точкой за интервал времени от t 1 = 0 с до t 2 = 3,0 с. Движение точки является равнозамедленным, поэтому необходимо выяснить, попадает ли точка остановки в указанный интервал.
Для этого запишем закон изменения скорости материальной точки с течением времени в виде:
v x = v 0 x + a x t = − 6,0 + 4,0 t ,
где v 0 x = −6,0 м/с - проекция начальной скорости на ось Ox ; a x = = 4,0 м/с 2 - проекция ускорения на указанную ось.
Найдем точку остановки из условия
v (τ ост) = 0,
т.е.
τ ост = v 0 a = 6,0 4,0 = 1,5 с.
Точка остановки попадает во временной интервал от t 1 = 0 с до t 2 = 3,0 с. Таким образом, пройденный путь вычислим по формуле
S = S 1 + S 2 ,
где S 1 = | x (τ ост) − x (t 1) | - путь, пройденный материальной точкой до остановки, т.е. за время от t 1 = 0 с до τ ост = 1,5 с; S 2 = | x (t 2) − x (τ ост) | - путь, пройденный материальной точкой после остановки, т.е. за время от τ ост = 1,5 с до t 1 = 3,0 с.
Рассчитаем значения координат в указанные моменты времени:
x (t 1) = 9,0 − 6,0 t 1 + 2,0 t 1 2 = 9,0 − 6,0 ⋅ 0 + 2,0 ⋅ 0 2 = 9,0 м;
x (τ ост) = 9,0 − 6,0 τ ост + 2,0 τ ост 2 = 9,0 − 6,0 ⋅ 1,5 + 2,0 ⋅ (1,5) 2 = 4,5 м;
x (t 2) = 9,0 − 6,0 t 2 + 2,0 t 2 2 = 9,0 − 6,0 ⋅ 3,0 + 2,0 ⋅ (3,0) 2 = 9,0 м.
Значения координат позволяют вычислить пути S 1 и S 2:
S 1 = | x (τ ост) − x (t 1) | = | 4,5 − 9,0 | = 4,5 м;
S 2 = | x (t 2) − x (τ ост) | = | 9,0 − 4,5 | = 4,5 м,
а также суммарный пройденный путь:
S = S 1 + S 2 = 4,5 + 4,5 = 9,0 м.
Следовательно, искомое значение средней путевой скорости материальной точки равно
v s = S t 2 − t 1 = 9,0 3,0 − 0 = 3,0 м/с.
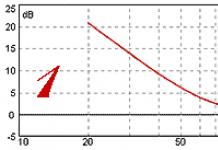
Пример 10. График зависимости проекции скорости материальной точки от времени представляет собой прямую линию и проходит через точки (0; 8,0) и (12; 0), где скорость задана в метрах в секунду, время - в секундах. Во сколько раз средняя путевая скорость за 16 с движения превышает величину средней скорости перемещения за то же время?
Решение. График зависимости проекции скорости тела от времени показан на рисунке.
Для графического вычисления пути, пройденного материальной точкой, и модуля ее перемещения необходимо определить значение проекции скорости в момент времени, равный 16 с.
Существует два способа определения значения v x в указанный момент времени: аналитический (через уравнение прямой) и графический (через подобие треугольников). Для нахождения v x воспользуемся первым способом и составим уравнение прямой по двум точкам:
t − t 1 t 2 − t 1 = v x − v x 1 v x 2 − v x 1 ,
где (t 1 ; v x 1) - координаты первой точки; (t 2 ; v x 2) - координаты второй точки. По условию задачи: t 1 = 0, v x 1 = 8,0, t 2 = 12, v x 2 = 0. С учетом конкретных значений координат данное уравнение принимает вид:
t − 0 12 − 0 = v x − 8,0 0 − 8,0 ,
v x = 8,0 − 2 3 t .
При t = 16 с значение проекции скорости составляет
| v x | = 8 3 м/с.
Данное значение можно получить также из подобия треугольников.
- Вычислим путь, пройденный материальной точкой, как сумму величин S
1 и S
2:
S = S 1 + S 2 ,
где S 1 = 1 2 ⋅ 8,0 ⋅ 12 = 48 м - путь, пройденный материальной точкой за интервал времени от 0 с до 12 с; S 2 = 1 2 ⋅ (16 − 12) ⋅ | v x | = 1 2 ⋅ 4,0 ⋅ 8 3 = = 16 3 м - путь, пройденный материальной точкой за интервал времени от 12 с до 16 с.
Суммарный пройденный путь составляет
S = S 1 + S 2 = 48 + 16 3 = 160 3 м.
Средняя путевая скорость материальной точки равна
v s = S t 2 − t 1 = 160 3 ⋅ 16 = 10 3 м/с.
- Вычислим значение перемещения материальной точки как модуль разности величин S
1 и S
2:
S = | S 1 − S 2 | = | 48 − 16 3 | = 128 3 м.
Величина средней скорости перемещения составляет
| v → r | = | Δ r → | t 2 − t 1 = 128 3 ⋅ 16 = 8 3 м/с.
Искомое отношение скоростей равно
v s | v → r | = 10 3 ⋅ 3 8 = 10 8 = 1,25 .
Средняя путевая скорость материальной точки в 1,25 раза превышает модуль средней скорости перемещения.
Способы задания движения точки.
Задать движение точки – это значит указать правило, по которому в любой момент времени можно определить её положение в заданной системе отсчёта.
Математическое выражение этого правила называется законом движения , или уравнением движения точки.
Существует три способа задания движения точки:
векторный ;
координатный ;
естественный .
Чтобы задать движение векторным способом , нужно:
à выбрать неподвижный центр;
à положение точки определить с помощью радиус-вектора , начинающегося в неподвижном центре и заканчивающемся в движущейся точке М;
à определить этот радиус-вектор как функцию от времени t: ![]() .
.

Выражение
![]()
называется векторным законом движения точки, или векторным уравнением движения .
!! Радиус-вектор – это расстояние (модуль вектора) + направление от центра О на точку М, которое можно определять разными способами, например, углами с заданными направлениями.
Чтобы задать движение координатным способом , нужно:
à выбрать и зафиксировать систему координат (любую: декартову, полярную, сферическую, цилиндрическую и проч.);
à определить положение точки с помощью соответствующих координат;
à задать эти координаты, как функции от времени t.

В декартовой системе координат, таким образом, надо указать функции

В полярной системе координат следует определить как функции от времени полярный радиус и полярный угол:

В общем, при координатном способе задания следует задавать как функции от времени те координаты, с помощью которых определяется текущее положение точки.
Чтобы можно было задавать движение точки естественным способом , нужно знать её траекторию . Запишем определение траектории точки.
Траекторией точки называется множество её положений за какой-либо промежуток времени (обычно – от 0 до +¥).
В примере с катящимся по дороге колесом траекторией точки 1 является циклоида , а точки 2 – рулетта ; в системе отсчёта, связанной с центром колеса, траектории обеих точек – окружности .

Чтобы задать движение точки естественным способом, нужно:
à знать траекторию точки;
à на траектории выбрать начало отсчёта и положительное направление;
à определить текущее положение точки длиной дуги траектории от начала отсчёта до этого текущего положения;
à указать эту длину как функцию от времени.

Выражение, определяющее указанную выше функцию,
называют законом движения точки по траектории , или естественным уравнением движения точки.
В зависимости от вида функции (4) точка по траектории может двигаться различным образом.
3. Траектория точки и её определение.
Определение понятия «траектория точки» был дано ранее в вопросе 2. Рассмотрим вопрос об определении траектории точки при разных способах задания движения.
Естественный способ : траектория должна быть задана, так что находить её не надо.
Векторный способ : нужно перейти к координатному способу согласно равенствам

Координатный способ : нужно из уравнений движения (2), или (3) исключить время t.
Координатные уравнения движения задают траекторию параметрически , через параметр t (время). Для получения явного уравнения кривой надо параметр исключить из уравнений.
После исключения времени из уравнений (2) получаются два уравнения цилиндрических поверхностей, например, в виде

Пересечение этих поверхностей и будет траекторией точки.
При движении точки по плоскости задача упрощается: после исключения времени из двух уравнений
уравнение траектории получится в одной из следующих форм:
![]()
![]()
![]()


При будет , поэтому траекторией точки будет правая ветвь параболы:


Из уравнений движения следует, что

поэтому траекторией точки будет часть параболы, расположенная в правой полуплоскости:


Тогда получим


Так как то весь эллипс будет траекторией точки.
При ![]() центр эллипса будет в начале координат О; при получим окружность; параметр k на форму эллипса не влияет, от него зависит скорость движения точки по эллипсу. Если в уравнениях поменять местами cos и sin, то траектория не изменится (тот же эллипс), но изменится начальное положение точки и направление движения.
центр эллипса будет в начале координат О; при получим окружность; параметр k на форму эллипса не влияет, от него зависит скорость движения точки по эллипсу. Если в уравнениях поменять местами cos и sin, то траектория не изменится (тот же эллипс), но изменится начальное положение точки и направление движения.
Скорость точки характеризует «быстроту» изменения её положения. Формально: скорость – перемещение точки за единицу времени .
Точное определение.

Тогда ![]() Отношение
Отношение

Механическим движением называют изменение с течением времени положения в пространстве точек и тел относительно какого-либо основного тела, с которым скреплена система отсчета. Кинематика изучает механическое движение точек и тел независимо от сил, вызывающих эти движения. Всякое движение, как и покой, относительно и зависит от выбора системы отсчета.
Траекторией точки называют непрерывную линию, описывае мую движущейся точкой. Если траектория - прямая линия, то движение точки называют прямолинейным, а если - кривая, то - криволинейным. Если траектория - плоская, то движение точки называют плоским.
Движение точки или тела, считается заданным или известным, если для каждого момента времени (t) можно указать положение точки или тела относительно выбранной системы координат.
Положение точки в пространстве определяется заданием:
а) траектории точки;
б) начала О 1 отсчета расстояния по траектории (Рисунок 11): s = О 1 М - криволинейная координата точки М;
в) направления положи тельного отсчета расстояний s;
г) уравнения или закона движения точки по траектории: S = s(t)
Скорость точки. Если точка за равные промежутки времени проходит равные отрезки пути, то ее движение называют равномерным. Скорость равномерного движения измеряется отношением пути з, пройденного точкой за некоторый промежуток времени, к величине этого промежутка времени: v = s/1. Если точка за равные промежутки времени проходит неравные пути, то ее движение называют неравномерным. Скорость в этом случае также переменна и является функцией времени: v = v(t). Рассмотрим точку А, которая перемещается по заданной траектории по некоторому закону s = s(t) (Рисунок 12):
 |
За промежуток времени t т. А переместилась в положение А 1 по дуге АА. Если промежуток времени Δt мал, то дугу АА 1 можно заменить хордой и найти в первом приближении величину средней скорости движения точки v cp = Ds/Dt. Средняя скорость направлена по хорде от т. А к т. А 1 .
Истинная скорость точки направлена по касательной к траектории, а ее алгебраическая величина определяется первой производной пути по времени:
v = limΔs/Δt = ds/dt
Размерность скорости точки: (v) = длима/время, например, м/с. Если точка движется в сторону увеличения криволинейной координаты s, то ds > 0, и следовательно, v > 0, а в противном случае ds < 0 и v < 0.
Ускорение точки. Изменение скорости в единицу времени определяется ускорением. Рассмотрим движение точки А по криволинейной траектории за время Δt из положения A в положение A 1 . В положении A точка имела скорость v , а в положении A 1 - скорость v 1 (Рисунок 13). т.е. скорость точки изменилась по величине и направлению. Геометрическую разность, скоростей Δv найдем, построив из точки A вектор v 1.
 |
Ускорением точки называют вектора ", равный первой производной от вектора скорости точки по времени:
![]()
Найденный вектор ускорения а может быть разложен на две взаимно-перпендикулярные составляющие но касательной и нормали к траектории движения . Касательное ускорение а 1 совпадает по направлению со скоростью при ускоренном движении или противоположно ей при замененном движении. Оно характеризует изменение величи-ны скорости и равно производной от величины скорости по времени
Вектор нормального ускорения а направлен по нормали (перпендикуляру) к кривой в сторону вогнутости траектории, а модуль его равен отношению квадрата величины скорости точки к радиусу кривизны траектории в рассматриваемой точке.
Нормальное ускорение характеризует изменение скорости по
направлению.
Величина полного ускорения: ![]() , м/с 2
, м/с 2
Виды движения точки в зависимости от ускорения.
Равномерное прямолинейное движение (движение по инерции) характеризуется тем, что скорость движения постоянна, а радиус кривизны траектории равен бесконечности.
То есть, r = ¥, v = const, тогда ; и поэтому . Итак, при движении точки по инерции ее ускорение равно нулю.
Прямолинейное неравномерное движение. Радиус кривизны траектории r = ¥, а n = 0, поэтому и а = а t и а = а t = dv/dt.